最短路径

发表于   |   分类于   |  

Floyd 算法分析

1
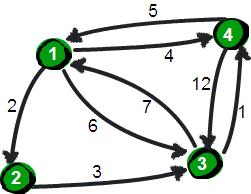
建立最短路径表格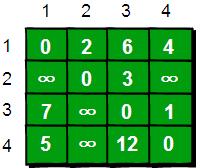
2
如果要让任意两点(a,b)之间的路径变短，只能引入第三个点K，并通过这个顶点K，转为a->k->b

接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。我们需要在只允许经过1号顶点时任意两点的最短路程的结果下，再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小，代码实现为如下。

1
2
3
4
5
6
7
8
//经过1号顶点   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
 if (e[i][j] > e[i][1]+e[1][j])  e[i][j]=e[i][1]+e[1][j];   
//经过2号顶点   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
 if (e[i][j] > e[i][2]+e[2][j])  e[i][j]=e[i][2]+e[2][j];

最后允许通过所有顶点作为中转，任意两点之间最终的最短路程为：

1
2
3
4
5
for(k=1;k<=n;k++)   
    for(i=1;i<=n;i++)   
 		for(j=1;j<=n;j++)   
     		if(e[i][j]>e[i][k]+e[k][j])   
   				e[i][j]=e[i][k]+e[k][j];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<stdio.h>
int ans[105][105];

int main()
{
	int N,M;
	while(scanf("%d%d",&N,&M)!=EOF)
	{
		if(N==0&&M==0)
			break;
		for(int i=1;i<=N;i++)
		{
			for(int j=1;j<=N;j++)
			{
				ans[i][j]=-1;
			}
			ans[i][i]=0;
		}
		while(M--)
		{
			int a,b,c;
			scanf("%d%d%d",&a,&b,&c);
			ans[a][b]=c;
			ans[b][a]=c;
		}
		for(int k=1;k<=N;k++)
		{
			for(int i=1;i<=N;i++)
			{
				for(int j=1;j<=N;j++)
				{
					if(ans[i][k]==-1||ans[k][j]==-1) continue;
					if(ans[i][j]==-1||ans[i][k]+ans[k][j]<ans[i][j])
					{
						ans[i][j]=ans[i][k]+ans[k][j];
					}
				}
			}
		}
		printf("%d\n",ans[1][N]);
	}
	return 0;
}