最长公共子序列

发表于   |   分类于   |  

· 这里是子序列，不是子串，所以不要求连续

初始状态与转换方程

1

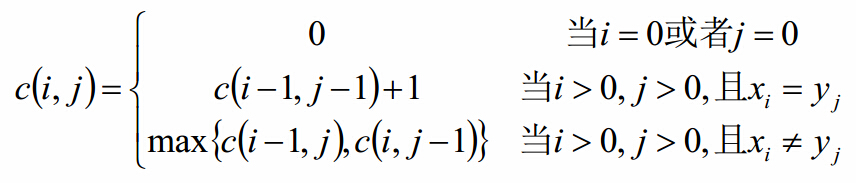
这里需要注意的事：

  • dp[i][j] 表示str1的前i项与str2的前j项的公共子序列的长度，所以如果i=0或j=0，dp[i][j]=0
  • 为了容易理解，我们设置数组str1与str2都是从1开始，这样,获取dp[i][j],即str1的前i项，与str2的前j项，就可以通过判断str1[i]与str2[j]获得。

最长公共子序列的获取

2
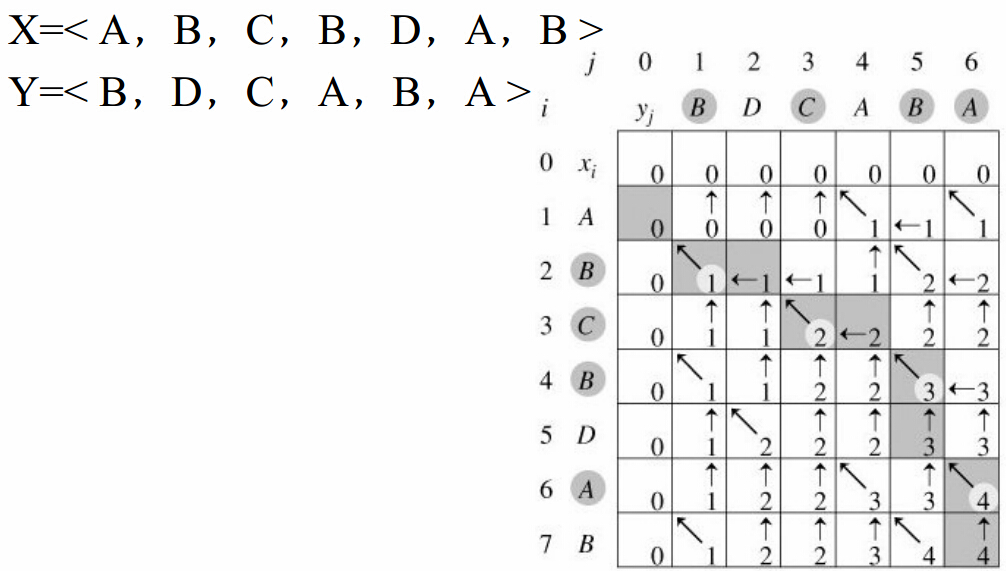
逆过程

  • 因为只有当str1[i]=str2[j]时，i和j同时增加，逆过程则同时减少
  • 正过程是dp[i-1][j]与dp[i][j-1] 谁大选择谁，逆过程则谁大谁减少
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<stdio.h>
#include<string>
#include<string.h>
#include<iostream>
#include<stack>
using namespace std;
stack<int> s;
int dp[100][100];
string LCS(char* str1, char* str2)
{
	int len1 = strlen(str1 + 1);
	int len2 = strlen(str2 + 1);
	for (int i = 0; i <= len1; i++)//i,j代表前几个字符进行比较,如果一方为前0个字符,则公共子序列长度为0
		//所以取值要在 (0,len]之间
	{
		dp[i][0] = 0;
	}
	for (int j = 0; j <= len2; j++)
	{
		dp[0][j] = 0;
	}
	for (int i = 1; i <= len1; i++)//这里的i,j代表前几个元素
	{
		for (int j = 1; j <= len2; j++)
		{
			if (str1[i] == str2[j])
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else
			{
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}
	int p = len1;
	int q = len2;
	while (p != 0 && q != 0)
	{
		if (str1[p] == str2[q])
		{
			s.push(str1[p]);
			p--;
			q--;
		}
		else if (dp[p - 1][q]>dp[p][q - 1])
		{
			p--;
		}
		else
		{
			q--;
		}
	}
	string lstr = "";
	while (s.empty() == false)
	{
		lstr += s.top();
		s.pop();
	}

	return lstr;
}

int main()
{
	char str1[100];
	char str2[100];
	while (scanf("%s%s", str1 + 1, str2 + 1) != EOF)//为了处理方便
	{
		string s = LCS(str1, str2);
		cout << s << endl;
	}
	return 0;
}