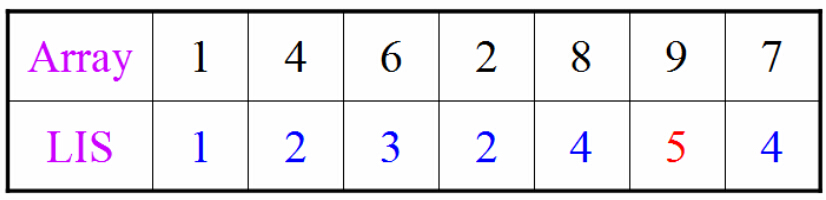
注意这里是子序列,不是子串,所以不要求连续。
初始化
- DP[i]=1 (所有i)
- DP[i]=max{DP[i],DP[j]+1| j<i&&a[j]<a[i]}
从前面的数组中找符合条件的,而不是根据最后一个只输出最长递增子序列的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23int LIS(char* str)
{
int len=strlen(str);
int *dp=new int[len];
for(int i=0;i<len;i++)
{
dp[i]=1; //最长递增子序列的最小值为1,即字符本身
}
int longest=1;
for(int i=1;i<len;i++)
{
for(int j=0;j<i;j++)
{
if(str[j]<=str[i])//这儿要根据题目,是否是严格递增
{
dp[i]=max(dp[i],dp[j]+1);
}
}
longest=max(dp[i],longest);
}
delete[] dp;
return longest;
}
输出最长递增子序列
这里需要一个前缀数组,保存子序列中每个字符的前一个字符的位置。初始化为-1,表示初始时每个字符都是独立的。
1 |
|