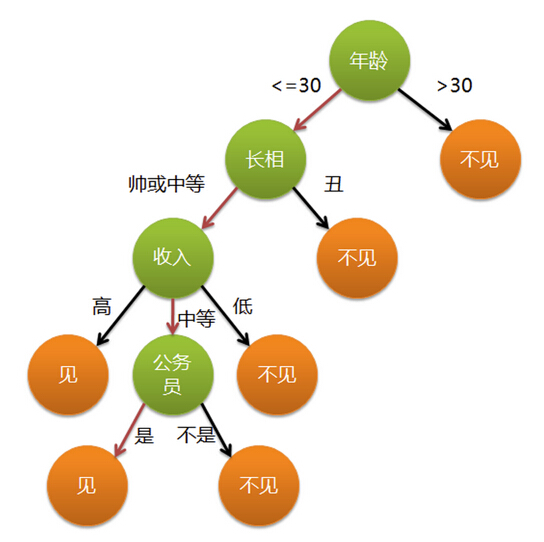
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这
个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
分裂属性
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。
属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
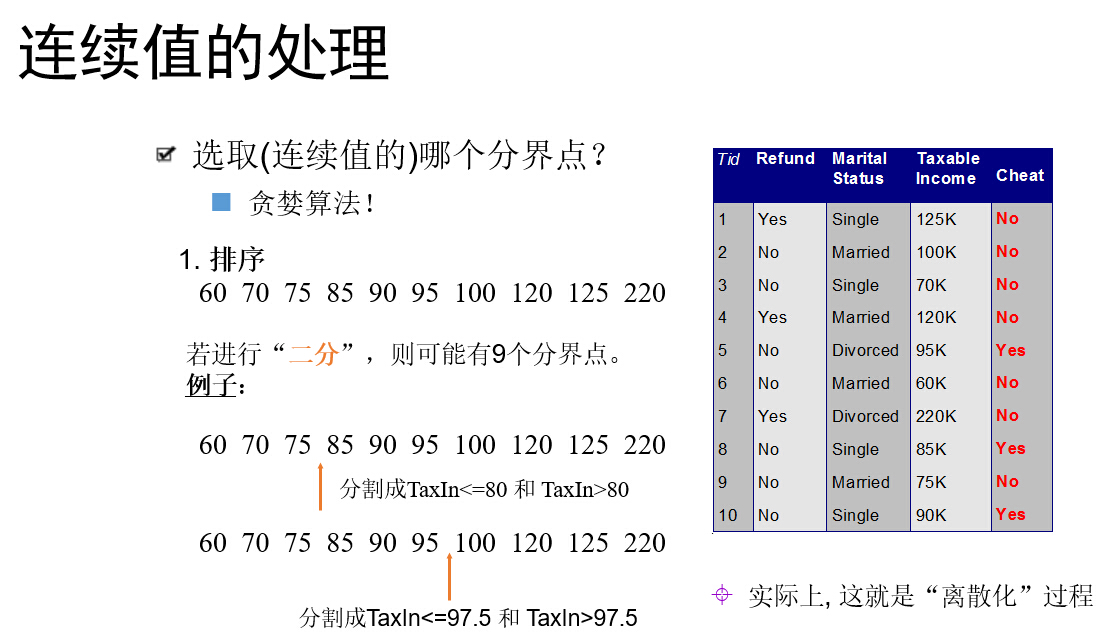
属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
信息熵
熵与信息内容的不确定程度有等价关系
平均信息量
若一个系统中存在多个事件E1,E2,…En
每个事件出现的概率是p1,p2,…pn
则这个系统的平均信息量是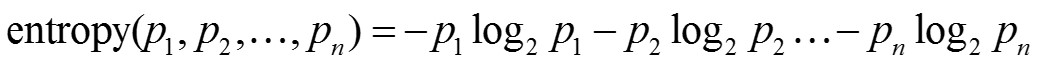
- 系统越无序、越混乱,熵就越大
- 通过分裂,得到尽可能纯的节点。这相当于降低系统的熵。
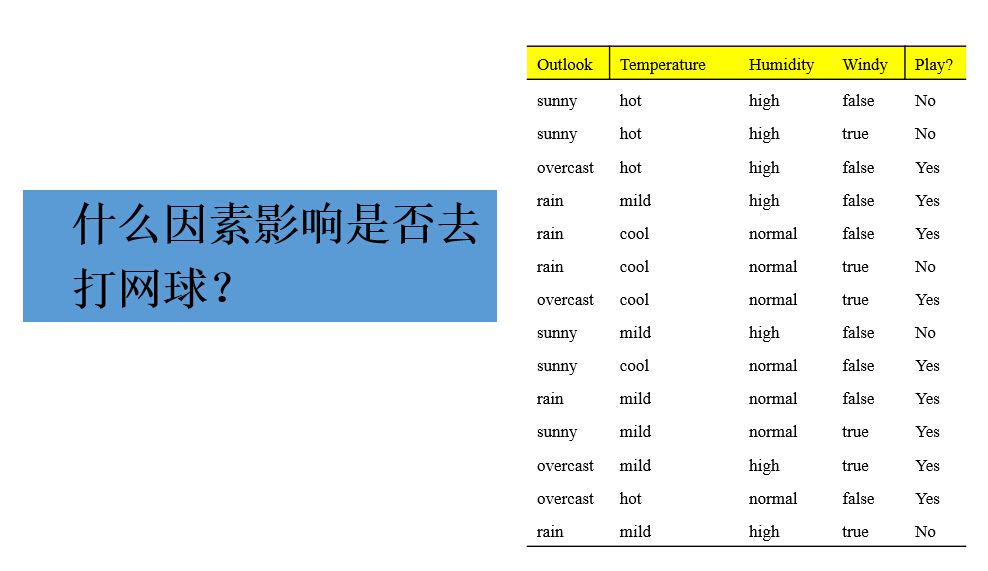
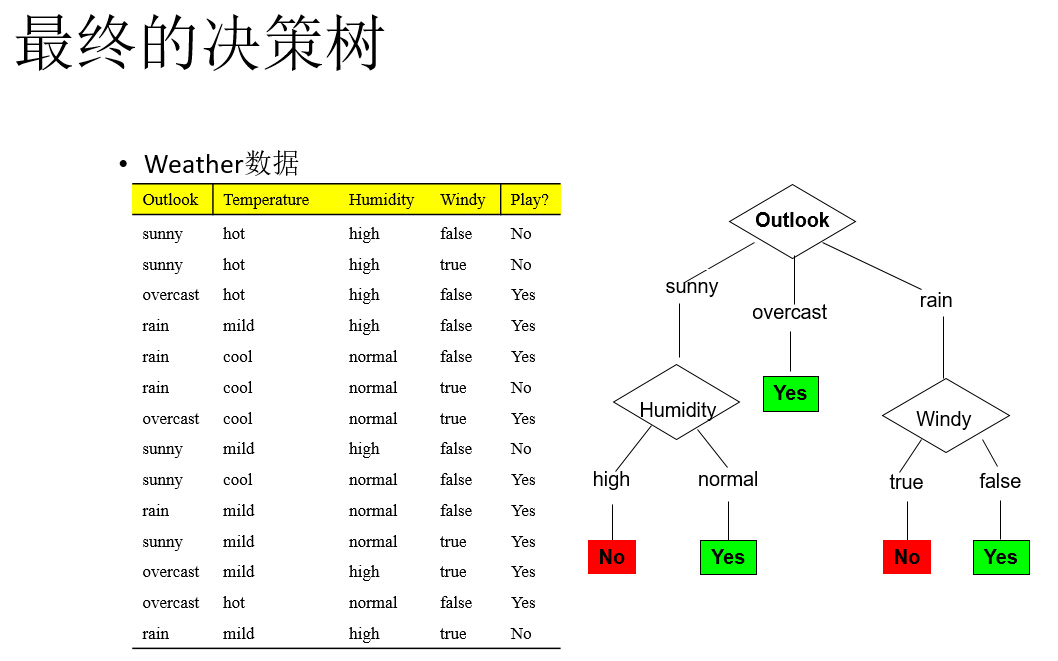
训练样本(用来创建树的数据集)在包含9个yes和5个no的根节点上,对应于信息值
info([9,5])=0.940bit →总的信息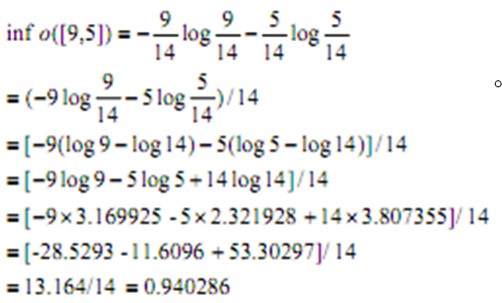
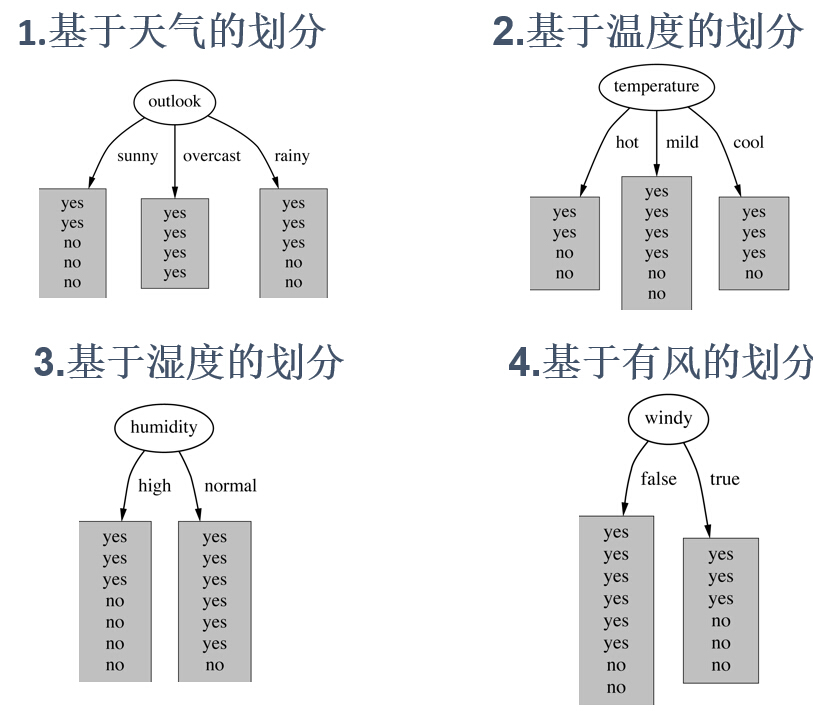
基于天气(outlook)的划分,在叶节点的yes和no类的个数分别是[2,3],[4,0],和[3,2],而这些节点的信息值分别是:
info([2,3])=0.971bit →sunny
info([4,0])=0. 0bit →overcast
info([3,2])=0.971bit →rain
根据天气的树导致的信息增益为:基于类比例原来信息需求-基于天气属性划分之后得到的信息需求
依次,计算每棵树导致的信息增益
为每个属性计算信息增益
gain(outlook)=0.247位
gain(temperature)=0.029位
gain(humidity)=0.152位
gain(windy)=0.048位
选择获得最大信息增益的属性进行划分
最大信息增益:gain(outlook)=0.247位
选择天气作为树的根节点的划分属性,其中一个子女节点是最纯的,并且这使它明显优于其他属性。
湿度是次佳选择,它产生了一个几乎完全纯的较大的子女节点。
以此类推,递归,继续划分
递归继续选择
当天气为晴时,所达到的节点上的可能的深一层的分支
除天气外,其他属性产生的信息增益
分别为:
gain(temperature)=0.571位
gain(humidity)=0.971位
gain(windy)=0.020位
继续再选择湿度(humidity)作为划分属性
当所有叶节点都是纯的,划分过程终止
理想情况下,当所有叶节点都是纯的而使过程终止时,即当它们包含的实例都具有相同类时该过程终止。
可能无法达到这种结果,因为无法避免训练集包含两个具有相同属性集,但具有不同类的实例。
当数据不能进一步划分时,停止划分过程。